Harvard Seismic Velocity Models

S2.9EA by Bogdan Kustowski, Göran Ekström, & Adam Dziewonski
S362MWANI by Bogdan Kustowski, Göran Ekström, & Adam Dziewonski
TOPOS362D1 by Yu Jeffrey Gu, Adam Dziewonski & Göran Ekström
S362D1 by Yu Jeffrey Gu, Adam Dziewonski, Wei-jia Su & Göran Ekström
SPRD6 by Miaki Ishii & Jeroen Tromp
BPD00 by Lapo Boschi & Adam Dziewonski
S20A by Göran Ekström, & Adam Dziewonski
BDP98 by Lapo Boschi & Adam Dziewonski
MK12_WM13 by Wei-jia Su & Adam Dziewonski
SKS12-WM13by Xian-Feng Liu & Adam Dziewonski
S12_WM13 by Wei-jia Su, Robert Woodward & Adam Dziewonski
M84A & M84C by John Woodhouse & Adam Dziewonski

1. S2.9EA
   

   

   Bogdan Kustowski, Göran Ekström, and Adam Dziewonski used a finer mesh for Eurasia and inverted for shear wave velocities and mantle transition zone topography. They parametrized Eurasia using lateral spacing of ∼ 2.9^° for spherical splines. The cross-section on the left shows S-wave velocity perturbation (color) and mantle transition zone topography (lines) between northern Adriatic Sea and Sea of Okhotsk.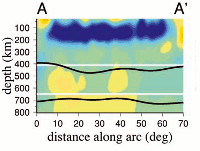
   
   [Download Model Coeffcients]   [Go to Project Web Site]
   
   
2. S362WMANI
   

   

   The depth slice on the left represent percent shear wave variation (V_SH-V_SV)/V_S at 300 km depth through the most recent Harvard mantle shear velocity model. Bogdan Kustowski, Göran Ekström, and Adam Dziewonski simultaneously inverted surface wave phase velocities, long-period waveforms and body wave travel times to obtain anisotropic shear velocity perturbations within the mantle.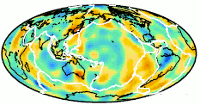
   
   [Download Model Coeffcients]    [Go to Project Web Site]
   
   
3. TOPOS362D1
   

   

   Yu Jeffrey Gu, Adam Dziewonski and Göran Ekström take a very important step and add mantle transition zone topography as a model parameter to their mantle shear velocity inversion. Mantle transition zone constraints come from the diffrential travel time measurements between SS, 410-km reflected S wave (S410S), and 660-km reflected S waves(S660S). The cross-section on the left represents the S-wave velocities (colors) and transition zone topography (thick lines) beneath South America, along a W-E cross-section.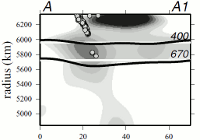
   
   [Download Model Coeffcients]    [Read Me]
   
   
4. S362D1
   

   

   
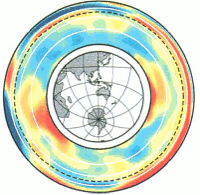
   Yu Jeffrey Gu, Adam Dziewonski, Wei-jia Su and Göran Ekström present a global shear velocity model for Earth's Mantle. They inverted absolute travel times (S, SS, and ScS), differential travel times (SS-S, ScS-S, S-KS, SKKS-SKS), body and mantle waveforms at different period, and Rayleigh and Love wave dispersion data. They used 362 spherical B-splines and 14 cubic B-splines for parametrization of the Earth in lateral and radial directions, respectively.
   
   [Download Model Coeffcients]    [Read Me]
   
   
5. SPRD6
   

   

   Miaki Ishii and Jeroen Tromp construct the first seismologically constrained whole mantle density model using normal-mode observations of several large magnitude earthquakes and Free-air gravity anomaly. Perturbations in shear velocity, bulk sound velocity, rigidity and incompressibility are compared with the models obtained by inverting travel-times and long perid body waveforms.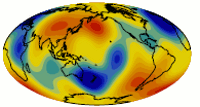
   
   [Go to Project Web-site]
   
   
6. BDP00
   

   

   Lapo Boschi and Adam Dziewonski updated the BDP98 model. They inverted P, PcP, PKPbc and PKPdf travel times to obtain lateraly and radially varying P wave velocity perturbations within the whole mantle. They used International Seismological Center bulletins from 1964 to 1993. Percent variation in horizontal P wave velocity (δV_PH/V_PH) at mid-mantle depths (1160-1353 km) are shown in the figure.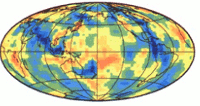
   
   [Download Model Coeficients]    [Read Me]
   
7. S20A
   
   

   

   
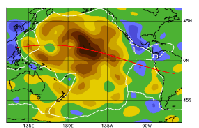
   In this study, Göran Ekström, and Adam Dziewonski investigated seismic anisotropy within the upper mantle beneath Pacific Ocean. They used travel-time data, complete long period waveforms at several frequency bands, and surface wave dispersion measurements within the period ranges of 35-150 s and 150-350 s.
   
   [Go to Project Web Site]
   
   
8. BDP98
   

   

   
   
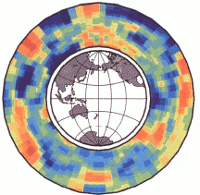
   Lapo Boschi and Adam Dziewonski compares the results of iterative and direct inversion techniques. Their tests involes LSQR, SIRT, Cholesky factorization for inversion, blocks and spherical harmonics for parametrization, and norm and roughness for regularization of the results. They present a P wave velocity model for the Earth's mantle using the data from the International Seismological Center bulletins between 1964 and 1992.
   
   [Download Model Coeffcients]   [Read Me]
   
   
9. MK12_WM13
   

   

   In this study, Wei-jia Su and Adam Dziewonski presents 3-D perturbations of shear velocity and bulk-sound velocity within whole mantle. Their model is defined using degree-12 spherical harmonics and 13th order Chebyshev polinomials in horizontal and radial directions, respectively. The data used in the inversion consist of:
   - 15,000 mantle-wave waveform
   - 25,000 body-wave waveform
   - 3,800,000 P wave travel-time
   - 60,000 PKPab travel-time
   - 520,000 PKPdf travel-time
   - 180,000 PKPbc travel-time
   - 67,000 S wave travel-time
   - ~14000 long period S, SS, SS-S, and ScS-S travel times
   
   [Download Model Coeffcients]    [Read Me]
   
   
   
10. SKS12_WM13
    

    

    
    
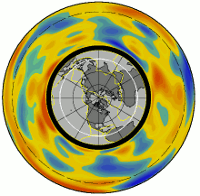
    S-wave ray paths are overlapped with the 3-D shear velocity model of SKS12-WM13. The source is located beneath the Sea of Okhotsk at around 500 km depth. Red and blue colors represent -3 % and +3 % velocity perturbation, respectively. They inverted travel time residuals of SS-S, ScS-S and S-SKS along with other absolute travel times and long period waveforms to obtain whole mantle S-wave velocity peturbation.
    
    [Download Model Coeffcients]    [Read Me]
    
    
11. S12_WM13
    
    

    

    
    
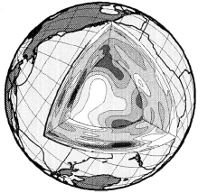
    Shear velocity perturbation beneath the Pacific Ocean is presented in black (+1.5 %) and white (-1.5 %). In this study, Wei-jia Su, Robert Woodward and Adam Dziewonski inverted about 27000 long period seismograms and around 14000 travel-time observations consisting of SS, SS-S and ScS-S readings.Since data coverage is considerably increased relative to the previous model, they used degree-12 spherical harmonics for lateral variations and 13th order Chebyshev polinomials for the radial perturbations.
    
    [Download Model Coeffcients]    [Read Me]
    
    
12. M84A & M84C
    

    

    The original paper by John Woodhouse and Adam Dziewonski is published in 1984. They presented a new approach to invert seismic waveforms to obtain 3-D shear velocity structure within the mantle. They used 87 events and around 870 different ray-paths. The final shear velocity model is expanded up to degree and order 8 in spherical harmonics (Model M84A) and corrected for crustal structure (Model M84C).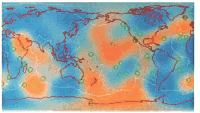
    
    [Download Model Coeffcients]    [Read Me]